If you have k numbers that add up to zero (with possible plus or minus signs), what is the maximum number ‘n’ of prime factors of the number with the least prime factors — what kind of inequality can we say about ‘n’ and ‘k’? The primes can be repeated, as long as there are no common factors for each term.

For example, 2*5*29 + 7*7*11 – 2*7*23 – 3*13*13 == 0 is true. In this case, n = 3 and k = 4. [In this case, the 12 primes are divided into four equal groups of 3, but that is not a requirement in general.]

MOTIVATION: the push and pull of multiplication and addition is an interesting topic. This seems a question in the same vein as Fermat’s Last theorem or the ABC conjecture, and it seems like a very natural similar question to ask. I suspect we’re not even close to being able to answer it, but would like to know if there’s a conjecture regarding ‘n’ and ‘k’, especially as they get larger, similar to the ABC conjecture inequality.

If you are in one of two identical lanes, then for the majority of the time you’ll be in the slower lane.

This fact does not spring from the psychology of human perception, but from mathematics. (The psychological aspect will enthusiastically add to our travails, of course.)

This violates our sense of symmetry, and so can be considered a paradox. The explanation of this paradox is not terribly sophisticated mathematically, although there are some subtleties to do with probability. However, to the best of my knowledge, it hasn’t been described elsewhere; at least, it isn’t familiar to most people. Since this situation comes up all so often, it seems it should be better known.

And it’s a nice little exercise in simple probability, too, so we’ll work it out in detail. Even if the result is obvious, there are some interesting aspects.

Here’s the article:

https://edgeofthecircle.net/lane_paradox.pdf

An article on that bizarre creature, the scorpionfly.

Click to access Scorpionfly.pdf

An article I wrote for the local friends of conservation newsletter

https://edgeofthecircle.net/beetle_pseudoscorpion.pdf

An article I wrote for the local friends of conservation newsletter

https://edgeofthecircle.net/ants_aphids.pdf

Faiz Ahmed Faiz’s poem, Nisaar mein teri galiyo ke, is one of my favorite poems. It has been on my mind a lot lately, for whatever reason. I ended up making my own rather loose translation. Sharing the translation first, then the original Urdu poem.

_____________________

A salute and a half to your alleyways, oh gracious land of mine,
Home to the latest fashion, that every head remain bowed!
Any discontent, any seeker who dares to venture about
May only slink through the streets with a tremble in their heart.
Those guilty of honesty soon learn the logic of the insane:
Attack dogs may roam free, only the bones of the earth are chained.

Those who deal out oppression need no more pretext
Than the handful of faithful who still whisper your name.
The lords of the land play both accuser and judge,
So who will defend you, from whom will justice flow?
But, for those who yet persist, the time yet drips away.
I’m absent now but listen, my love: these days will slip away.

When the door of the jail grows dark, it’s the heart that can see
How the stars of the sky are now scattered in your mane.
When the chains that bind me are lit, what I perceive
Is the glow of dawn upon your face.
Prison’s days are but mirages of sun’s rises and its falls.
My life crawls captive to the shadows of the walls.

Oh, this is the way of the war of the tyrants and the people.
There’s nothing novel in their rites, nothing novel in our fight.
We can coax roses to bloom from the very midst of the blaze,
So their loss will come soon, and our successes no surprise.
Why should I complain about a little time in the dark?
In this short moment I’m away, I won’t shadow my heart.

So this day we’re apart, the morrow we’re together.
A parting of but one night is no matter at all.
If the oppressor’s fist is now high, it’s really no bother.
This silly half-week of their might is no matter at all.
Those who remember their truths, who hang fast to their reasons,
Hold the power to halt these petty whirlpools of seasons.

Original:
Nisaar mein teri galiyon ke ai watan ke jahan,
Chali hai rasm ke koi na sar utha ke chale,
Jo koi chahne waala tawaaf ko nikle,
Nazar chura ke chale, jism-o-jaan bacha ke chale,
Hai ahl-e-dil ke liye ab ye nazm-e-bast-o-kushaad,
Ke sang-o-khisht muqayyad hain aur sag aazaad.

Bahut hai zulm ke dast-e-bahaana-joo ke liye,
Jo chand ahl-e-junoon tere naam lewa hain,
Bane hain ahl-e-hawas mudd’ai bhi, munsif bhi,
Kise wakeel karein, kisse munsifi chahein,
Magar guzaarne waalon ke din guzarte hain,
Tere firaaq mein yoon subh-o-shaam karte hain.

Bujha jo rozan-e-zindaan to dil ye samjha hai,
Ke teri maang sitaaron se bhar gayi hogi,
Chamak uthe hain salaasil to hum ne jaana hai,
Ke ab seher tere rukh par bikhar gayi hogi,
Gharaz tasavvur-e-shaam-o-seher mein jeete hain,
Giraft-e-saaya-e-deewaar-o-dar mein jeete hain.

Yoon hi hamesha ulajhti rahi hai zulm se khalq,
Na unki rasm nayi hai, na apni reet nayi,
Yoon hi hamesha khilaaye hain hum ne aag mein phool,
Na unki haar nayi hai, na apni jeet nayi,
Isi sabab se falak ka gila nahi karte,
Tere firaaq mein hum dil bura nahi karte.

Gar aaj tujh se juda hain to kal behem honge,
Ye raat bhar ki judaai to koi baat nahi,
Gar aaj auj pe hai taala’-e-raqeeb to kya,
Ye chaar din ki khudai to koi baat nahi,
Jo tujh se ehd-e-wafa ustuwaar rakhte hain,
Ilaaj-e-gardish-e-lail-o-nihaar rakhte hain!

This book is intended for two types of people: those who love mathematics, and those who don’t. If you belong to either one of these groups, I hope you will read on.

The mathematics that most people encounter (high school, typically) isn’t a reflection of what higher math is like. This means that people decide whether or not they like mathematics, without ever knowing what mathematics is like.

This book is a journey along the paths of mathematics as it can be. It’s aimed at someone with an approximately high school level of knowledge (or you could be a really motivated middle schooler, that’s okay too!) , with no knowledge of calculus, matrices, or complex numbers assumed.

At the same time, I wanted this to be a book of mathematics, rather than a book about mathematics. What does that mean? You’re not going to be reading about concepts and proofs that other people did, you’re going to be actually taking the steps yourself. And yet, we’re going to actually reach some pretty sophisticated destinations.

To use mountaineering as a metaphor: this book is a hike to the top, as opposed to a technical rock-face climb. It’s easier and doesn’t need as much training, but you’re still going to take the steps yourself to get to the top. And you get to enjoy the view at the end that you arrived at by yourself, rather than look at a photo that someone else took.

https://edgeofthecircle.net/living_mathematics.pdf

CO2 reduction strategies comparison

Common strategies and common sense in carbon dioxide reduction

Please note, this is a work in progress. I will continue to update as I get time!

A cost-benefit comparison of some things that you can do to stop global warming

---

1. Introduction

1.1 Motivation

Have you ever been to a restaurant that didn’t put the prices on its menu?

There are many things we can do to help the environment, and help stop global warming. Here’s something that’s more difficult: to decide what the best ways are, what the most cost-effective ways are, instead of going in blind. Lacking good data, there’s that uneasy feeling, as if we just sat down to order at a restaurant that chose not to list the prices.

I couldn’t find a reasonable cost-benefit analysis of many of the actions we could take. So I’m going to try to do the calculations myself.

The main metric will be dollars spent per tonne of CO₂ saved; I will also calculate the dollar cost for the average person (in a first-world country) to reduce their CO₂ consumption down to the annual CO₂ budget, if we were to use that strategy alone.

There will be other actions that we can take that do not fit into this analytical framework of dollars/tCO₂, but we can still try to quantify how much CO₂ they save, to help us decide whether the actions are worth taking or not.

This is not intended to be a discussion of cutting edge research. Instead, the point is to focus on actions that can be taken by most of us.

1.2 Disclaimer

Here are my credentials for this task: I don’t have any.

Don’t take my word for anything. I’ll try to show my calculations, so if there are any mistakes it should be easy to point them out. All corrections and suggestions gratefully accepted.

1.3 The ideas I looked at

Here’s a list of some of the possible actions that were considered.

1. Hybrid cars
2. Electric cars
3. Buying a smaller car
4. Heat-sink (“geothermal”) AC/heating
5. Tankless water heaters
6. Rooftop solar panels
7. Green electricity from the power grid
8. Saving forests or planting trees
9. Carbon offsets
10. Carbon capture
11. Biofuels
12. LED bulbs
13. House insulation
14. Energy efficient appliances
15. A vegetarian diet
16. Local food
17. Cycling instead of driving
18. Flying less often

---

2. Summary

(In case you have dinner cooking on the stove and don’t want to read too much further.)

This table summarizes the results, so you don’t have to read the details below if you don’t want to. For each strategy, it provides the following information:

1. cost, using two different metrics: (a) dollars per tonne of CO2, and (b) the amount it would cost to go from the average US person to bring their CO2 consumption down to a sustainable carbon budget
2. cost or savings using other measures, for strategies that don’t fit the $/tCO2 metric
3. additional benefits and drawbacks that can’t be quantified easily

S. No.	Strategy	Savings	Other benefits and drawbacks
1	Hybrid cars: in this case, hybrid Civic vs. regular Civic	$100/tCO2, 3 months carbon budget / $100	Hybrid batteries use rare-earth metals, have environmental consequences
2	Toyota Highlander, hybrid vs regular	$800/tCO2, 12 days carbon budget / $100	Hybrid batteries use rare-earth metals, have environmental consequences

---

3. Some useful numerical values

Parameter	Value	References	Comments
CO2 budget per person	Approximately 3 tonnes per person	link	In most plans, the carbon budget starts higher and gradually drops. 3 tonnes per person is a very rough approximation of the midpoint of this process. This is the combined emissions from personal spending on housing, travel, food, products and services.
CO2 produced per capita, per year	Approximately 16 tonnes per person, per year (USA)	link	For comparison, approx 5 tonnes per person per year (China), 1 tonne per person per year (India)
Effect of carbon taxes	A tax of $25/tCO2 would add 21 cents per gallon to the price of gasoline, 1.2 cents per kW-hour for electricity from non-renewable sources.	link	Please note that carbon taxes have severe flaws as way of remediating damage due to global warming. See chapter 4 of this article, or also this discussion: link
CO2 emission per unit of electricity	4.5 × 10-4 tonnes/kW-hour	link	This calculation does not include line losses, or other gases such as methane. These are not significant at the level of accuracy that we will be working with.
CO2 per liter of gasoline burned	2.2 × 10-3 tonnes CO2 per liter	link	8.9 × 10-3 tonnes CO2 per gallon
CO2 to carbon conversion	3.7 tonnes of CO2 = 1 tonne of C	Ratio of the atomic weight of CO2 to the atomic weight of C	Some sources give the carbon budget, while others give the CO2 budget. This is useful in converting between them. We will use CO2 for all calculations.
CO2 per kilometer of air travel	0.2 kg CO2 per mile (!)	link

4. Why should we care?

Obviously, this section is more personal and less quantitative. And it’s not the purpose of this article to get into details of the enormous effects of global warming on people and the environment. There’s already plenty of research about that, for example here and here and here and here and here.

However, I would like to point out is that pure economic analyses of the costs of global warming are inadequate; and that levying carbon taxes as a way of solving the problem can also be inadequate. A lot of the analyses of the effects of global warming actually understate the moral imperative to combat it, especially by residents of first-world nations.

1. There are huge non-economic affects of global warming, such as habitat loss and species extinction.
2. Global warming is not just shunting money from poorer regions to wealthier ones. It’s shunting money from the victims of global warming to the agents of global warming.
3. Related to the previous point, the financial estimates of the harm done are not commensurate with the actual devastation. For example, take someone who gets two meals a day: if they are deprived of one of these meals, this gets counted as just a dollar or two of harm, but the actual damage would be considerable.
4. The people who are harmed do not have the choice whether or not to accept the change to their lives. For example, they may be forced to move from a land where they have lived for many generations, or abandon the only livelihood they know how to make; this is a fundamental uprooting that most of them would prefer not to do, whether or not they are compensated for it.
5. Borders are not open. Climate change may lead to some areas being less habitable and other areas more, with a smaller net effect. However, people who are badly affected do not have the choice to move to other places, even if they wanted to.
6. The money collected by carbon taxes is not distributed to the people who are most harmed by the affects of global warming. In particular, the tax money goes to the government where the economic activity happens, but the harmful effects are felt worldwide, and predominantly in regions with lower economic activity. So even with a carbon tax, there is a net effect of shunting money from poorer regions to wealthier ones.
7. The numbers actually used as carbon taxes in practice are influenced heavily by political factors separate from the actual social cost of the carbon. In particular, it cannot be set more than can be accepted by the politicans and populace.
8. The carbon tax is considered by many politicians to have repercussions on the economy, and is set lower than the expected social cost of carbon in order to take these repercussions into account.
9. Once the changes from global warming have been effected, they can last a very long time, accumulating damage. Therefore, actual prevention is much more valuable than remediation.
10. The estimates of the cost of global warming that carbon taxes are based on, are calculated by discounting future costs. That is, something that would harm a future generation $100, is given a cost of, say, $50, as it is assumed that we do not care as much about affects in the future. The moral hazards of this should be obvious.

5. Calculations for individual cases

5.1 Hybrid cars and other fuel-efficient cars:

5.1.1 Honda Civic vs. Honda Civic Hybrid

Assume that the fuel efficiency of a hybrid car (such as a Toyota Prius or a Honda Civic hybrid) is 50 miles/gallon 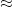20 km/liter of gasoline, and that a gasoline-driven Honda Civic gets 35 miles/gallon, which is about 14 km/liter.

There are a couple of different ways of calculating this. We’ll do it both ways to see if they agree with each other as a sanity check. The first is by using “true cost of ownership” from Kelly Blue Book (kbb.com) or Edmunds (edmunds.com) to determine the costs, while the second is by simply using the upfront costs. The first method aims to be more accurate, while at the same time has more assumptions built into it.

5.1.1.1 Calculation using “true cost of ownership”

We will do the calculations for a distance driven of 75,000 miles, which is 120,000 km. (The reason for choosing this particular number is that Edmunds calculates the total cost of ownership over this distance.)

Over this distance, the car will use approximately 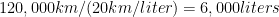of gasoline. This translates into 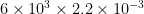tonnes of CO₂ over the lifetime of the vehicle, or 13.2 tonnes of CO₂.

For a conventional car, the number of tonnes of CO₂ over the calculation period of the car would be 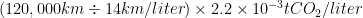= 19 tonnes of CO₂.

Therefore, the savings of gasoline over 120,000 km are 6 tonnes of CO₂.

To find the dollar cost for that savings in gasoline, we will use the Edmunds total cost of ownership. For that distance (5 years at 15,000 miles per year), the total cost of ownership for the Honda Civic is $32,000, while that for a Honda Civic Hybrid is $33,300.

Therefore, the cost per tonne of CO₂ is (33,300 – 32,000)/6 = $200/tonne of CO₂.

5.1.1.2 Calculation using direct costs

Assume that the life of the car is 150,000 mi or 250,000 km.

Number of tonnes of CO₂ over this lifetime for a regular car: 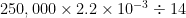= 40 tCO₂.

For a hybrid, by the same calculations, this number is 27.5 tCO₂. So the difference is approximately 12 tCO₂.

From Edmunds.com, we estimate the extra cost of a hybrid at $5,000. We will assume that the price of gas is $3/gallon.

Over the full lifetime of 150,000 miles, the gasoline car will use 150,000/35 = 4300 gallons of gasoline. The hybrid will use 150,000/50 =3000 gallons.

The savings in gas will recoup 1300 * 3 = $3900 dollars of the difference in cost. The savings in CO₂ emissions will be .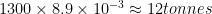

By this calculation, the efficiency of buying a hybrid is 100/tCO₂$. These calculations are very sensitive to the difference in price; if it were $6000 rather than $5000 the answer would be approximately $200/tCO₂.

5.1.2 Toyota Highlander vs Toyota Highlander Hybrid

This cost per tonne is very sensitive to the gas mileage of the cars. It makes sense to repeat this calculation for a “typical” SUV. We choose the Toyota Highlander.

mileage	total cost of ownership (120,000 km)	tonnes of CO2 (120,000 km)
Toyota Highlander	18/24 mpg	$41,903	33 tonnes CO2
Toyota Highlander Hybrid	28 mpg	$49,878	23 tonnes CO2

This gives a cost per tonne of CO₂ of (50,000-42,000)/(33-23) = $800/tCO₂. Note that if we use Kelley instead of Edmunds, it is $600/tCO₂.

5.1.3 Drawbacks other than CO₂ emissions

There are significant drawbacks to hybrid and electrical cars that are not reflected here: batteries can be pretty messy and energy intensive to manufacture. By most analyses, this extra cost to manufacture is not large compared to the savings from the added energy efficiency ([4], [5]).

5.2 Electric cars

For electric cars, there are two important cases to consider: the electrity can come from fossil fuels, or it can come from renewable (carbon-neutral) sources.

The carbon cost of an electric car comes from two parts: the cost to manufacture, and the carbon cost of the electricity. For hybrid and gasoline cars, the second cost dominates, but for electric cars both have to be taken into consideration ([4], [5]). Note that if the manufacturer derives its electricity from renewable sources, that part also vanishes, but we assume that this is not the case.

5.2.1 Charging from fossil fuel sources

The ratings for US electric cars are given in MPGe, or miles per gasoline equivalent: the distance travelled for a charge of electricity equivalent to the energy of one gallon of gasoline. This amount of energy is 33.7 kW-hours.

Remember that carbon cost of electricity is 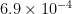tonnes of CO₂ per kW-hour.

We will choose the Nissan Leaf as a representative for electric cars. For this vehicle, the fuel economy is 114 MPGe, or 30 kW-hours/100 mi.

For this vehicle, the Edmunds True Cost to Own for the standard 5 year/15,000 miles per year situation is $23,000. This takes into account a tax credit of $7,500. The Kelley Blue Book estimate of the total cost of ownership is $35,835, which is $28,000 if you consider the tax credit. We will choose a value of $25,000.

It’s tough to decide what exactly to compare this to. We’ll choose a Honda Civic as the closest equivalent. As mentioned above, the Edmunds True Cost to Own is $32,000, and it emits 19 tonnes of CO₂ over the calculation period.

For the Nissan Leaf, the amount of CO₂ emissions to travel 75,000 miles is 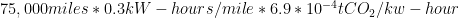. This is 15.75 tonnes of CO₂.

So the Nissan Leaf gets 114 miles per energy equivalent of a gallon of gasoline, while the Honda Civic Hybrid gets 45 miles per gallon of gasoline, yet the Nissan Leaf creates approximately the same CO₂ emissions per mile. This was certainly a surprise. Presumably this has to do with the inefficiencies of burning fossils fuels and converting to electricity — or the numbers used from the EPA, for CO₂ emitted per gallon of gasoline and per kW-hour of electricity, may be inaccurate. Also note that this disagrees with the numbers from the reference [5], but I don’t know how they obtain their numbers.

(As a check of this rather startling conclusion, note that one gallon of gasoline is equivalent to 33.7 kW-hours of electricity. So the amount of CO₂ emissions per 1MW-hour of gasoline is 8.9 kg CO₂/gallon * 1 gallon/33.7 kW-hours * 1000 kW-hours/1MW-hour * 1 tonne/1000 kg = 0.26 tonnes/MW-hour. But the value used for electricity is 0.69 tonnes/MW-hour. I do not have an explanation why electricity is so much more expensive other than inefficiencies of generation and conversion.)

Therefore, over a 75,000 mile ownership, the Nissan Leaf saves $7,000 and also saves approximately 3 tonnes of carbon dioxide. If the $7,500 tax credit is taken away, owning a Nissan Leaf has an efficiency of $500/3 = $166/tCO₂. Again, this number is extremely sensitive to the estimate of the total cost of ownership, and also the cost of the car we’re comparing it with, so this number does not have a high degree of significance. It does, however, seem robust to say that the price of the car is competitive with comparable cars, and will save a few tonnes of CO₂.

5.2.2 Charging from renewable sources

Of course, the electricity used for recharging the electric car batteries may be obtained from renewable sources. In this case, the only emissions are those used in producing the car and battery. The above reference provides a value of 8.8 tCO₂ for this, which is approximately 3 tCO₂ more than for a gasoline powered car.

However, note that the cost of electricity will then be slightly higher, thereby increasing the total cost of ownership.

Over 150,000 miles, the number of kW-hours used would be 150,000 miles * 0.3 kW-hours/mile = 45,000 kW. The average price of electricity per kilowatt-hour in the US is $.13/kW, rising to $.20/kW in New England (see [6]. If we choose to use electricity sourced from green sources, the extra cost is 2.4 cents per kilowatt-hour.

5.3 Heat Sink (“Geothermal”)

Make an estimate of the savings in terms of gas; find the amount of gas used without this; and electricity for air-conditioning. How much extra electricity gets used? We will need the lifetime of a system. Check the book, and the article mentioned in the email.

5.4 Solar panels

Costs of making it, including environmental costs, and water.

Lifetime of solar panels

Total energy output over lifetime

Cost per kilowatt-hour of the electricity.

co2 saved.

5.5 Green electricity from the grid

Cost per unit of electricity with and without.

co2 per unit of electricity.

5.6 Saving forests

Cost of buying a hectare of rain forest. Amount of carbon in the hectare of rain forest. What is the probability that, if you hadn’t bought it, it would have been cut down? Can we assume that the higher that probability is, the more valuable the land is, so choose a value along the upper part of the range? This does make some sense; using the value of the land as a proxy for the likelihood it will be used for other purposes. We could additionally use a value for this probability based on how fast the rain forest is disappearing.

Carbon in the hectare of rain forest, we may be able to assume that if the trees were cut down, there would be one meter of wood on the ground?

Need the carbon content of each kilo of organic material.

Mention very large benefits in terms of non-climate change environmental factors.

---

Look at TED talk about how this is one of the best methods.

---

There are also estimates of how much carbon each hectare of forest processes per year. This seems strange, because it doesn’t mention how much is released by bacteria or termites breaking down the dead wood. Maybe find out how accurate this estimate is. In case you want to look at this, then you can estimate the annual cost of a hectare of rainforest by doing a cost of house to rent conversion, and applying that to the cost of a hectare of forest.

5.7 Carbon credits

cost of carbon credits (also look for carbon offsets).

where do they come from? cap and trade?

are they any good?

Probably a complete fraud. But look at how they work, how much they cost per tonne of carbon.

5.8 Biofuels

I’m not sure what I meant. Wood burning? Corn ethanol? This is tough to quantify and may make sense to skip.

5.9 LED bulbs

Life of led bulb. Life of ordinary bulbs. Amount of energy used over life of led bulb. Energy used over life of ordinary bulbs. Difference in cost of bulbs, energy. Co2 expenditure.

5.10 House Insulation

Yay, we got some info on that. Also do your own calculations, starting from the average heating costs.

5.11 Energy efficient appliances

5.12 Vegetarian Diet

5.13 Local food

5.14 Cycling

5.15 Flying less often

---

I recently got bored and decided to try to find a proof of the Basel Sum. In an unexpected departure from tradition, I actually found one. As a further surprise, it seems to be a lot simpler than any other proof I’ve seen: just a few steps, and each one pretty obvious.

A reminder: the Basel sum states that

   

And an important clarification: this proof is “original”, in the sense of I came up with it myself, yay, but most definitely not original in the sense of I was the first to come up with this proof. The Basel sum is exceedingly well traveled territory mathematically, and I would be surprised if I was in the first 1000 people to come up with this proof independently.

Before we start the proof, a reminder of the definition of the double factorial. For an even number , . Similarly, for an odd number , . And we can choose to define .

Step 1:

Let

   

Then,

   

Subtracting these two equations, we get

(1)  

Step 2:

(2)  

This is easy to prove by induction, using integration by parts.
Click here for the proof, if you really, really want it. But you probably don't.

Step 3:
Start with the Taylor series for :

   

Note that this is absolutely convergent. Now simply substitute .

(3)  

Step 4:
In equation (3), integrate from to .

   

Step 5:
So the RHS is what we looked at in equation (1). This means

   

so

(4)  

Addendum: I did some more research. Euler himself did something very similar (here). The earliest version of this exact proof that I could find was by Boo Rim Choe in the American Mathematical Monthly in 1987 (Vol. 94, No. 7 (Aug. – Sep., 1987), pp. 662-663 ).

The raven's
Not painted
  -- Yet flies!

A friend
Far away
Remembers